Internet Scholar

Easily solve lagrange s method of multipliers with one subsidiary condition good example part 2 duration. In general the lagrangian is the sum of the original objective function and a term that involves the functional constraint and a lagrange multiplier λ.

Lagrange Multiplier Example Part 1 Video Khan Academy

This is the currently selected item.

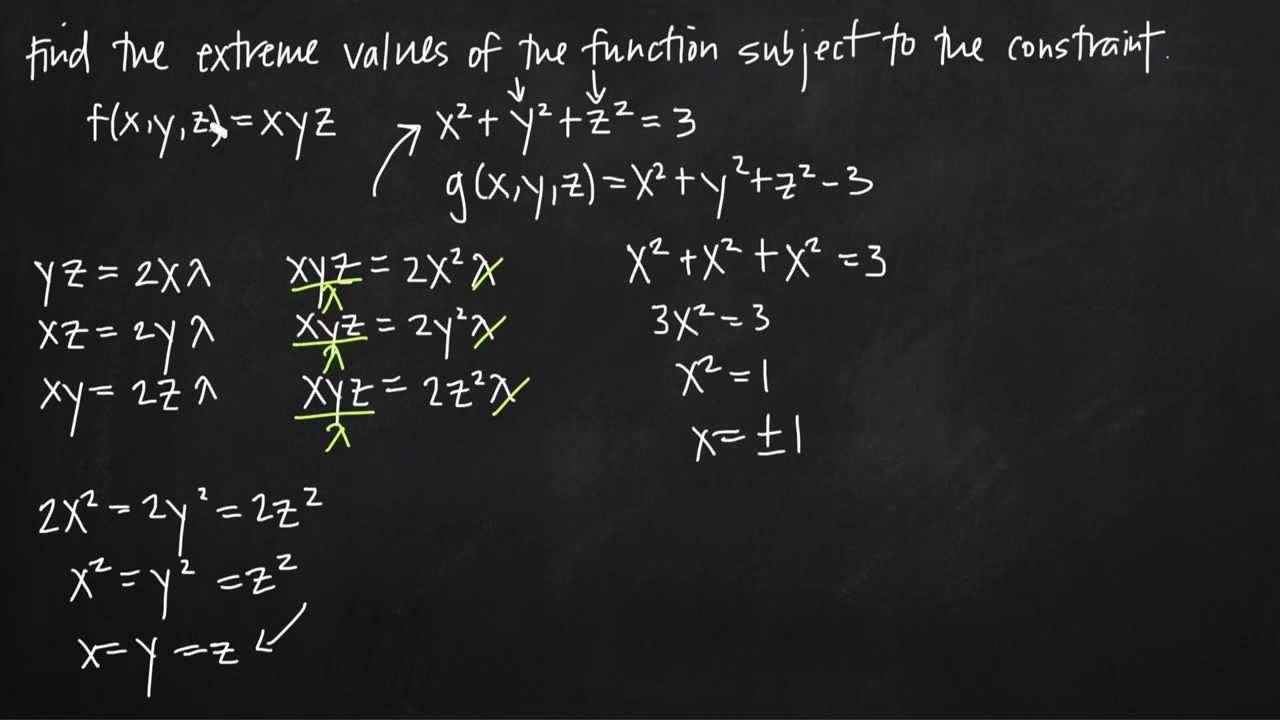
Lagrangian function economics example. Lagrange multiplier example part 1. Multiply the constraints by the factors lambda one and lambda two ë 1 and ë 2 respectively more on these in a moment. In addition there are two constraints c 1 and c 2 that are also functions of x and z.

Meaning of the lagrange multiplier. Examples of the lagrangian and lagrange multiplier technique in action. If you re seeing this message it means we re having trouble loading external resources on our website.

Easy maths easy tricks 4 344 views. For example the consumer s choice problem can be represented by either fixing a budget and obtaining its maximum utility primal demand or by setting a level of utility we want to achieve and minimise cost dual demand. Lagrange multipliers finding maximum or minimum values duration.

Finishing the intro lagrange multiplier example. For example in economics the optimal profit to a player is calculated subject to a constrained space of actions where a lagrange multiplier is the change in the optimal value of the objective function profit due to the relaxation of a given constraint e g. Through a change in income.

For the example of the next subsection where the function f is the production function the lagrange multiplier is the marginal product of money. And we introduce the lagrangian function constrained optimisation plays a central role in economics. The following steps establish the lagrangian function.

Suppose we ignore the functional constraint and consider the problem of maximizing the lagrangian subject only to the regional constraint. Respecify the constraints so that they equal zero. Lagrange multiplier example part 2.

Lagrange multipliers if f x y is a sufficiently smooth function in two variables and g x y is another function in two variables and we define h x y z f x y zg x y and a b is a relative extremum of f subject to g x y 0 then there is some value z λ such that h x a b λ h y a b λ h z a b λ 0. In such a context λ is the marginal cost of the constraint and is referred to as the shadow price. Proof for the meaning of lagrange multipliers.

In section 19 1 of the reference 1. Lagrange multipliers using tangency to solve constrained optimization.